Watching the guards: Developing a Web-Based Alarm System for Early Detection of SARS-CoV-2 in Sewage Using Principal Component Analysis and Threshold Trespassing

Ll. Bosch1,2, J. Pueyo1,2, M. Comas2, M. Calvo3, J. Saldaña2, J. Ripoll2, E. Calle2, C. Borrego1,2, Ll. Corominas1,2,*

1: Catalan Institute for Water Research (ICRA), Emili Grahit 101, 17003 Girona, Spain
2: University of Girona, Plaça Sant Domènec 3, 17004 Girona, Spain
3: University of Barcelona, Gran Via de les Corts Catalanes 585, 08007 Barcelona, Spain
*: Corresponding author: Lluís Corominas lcorominas@icra.cat

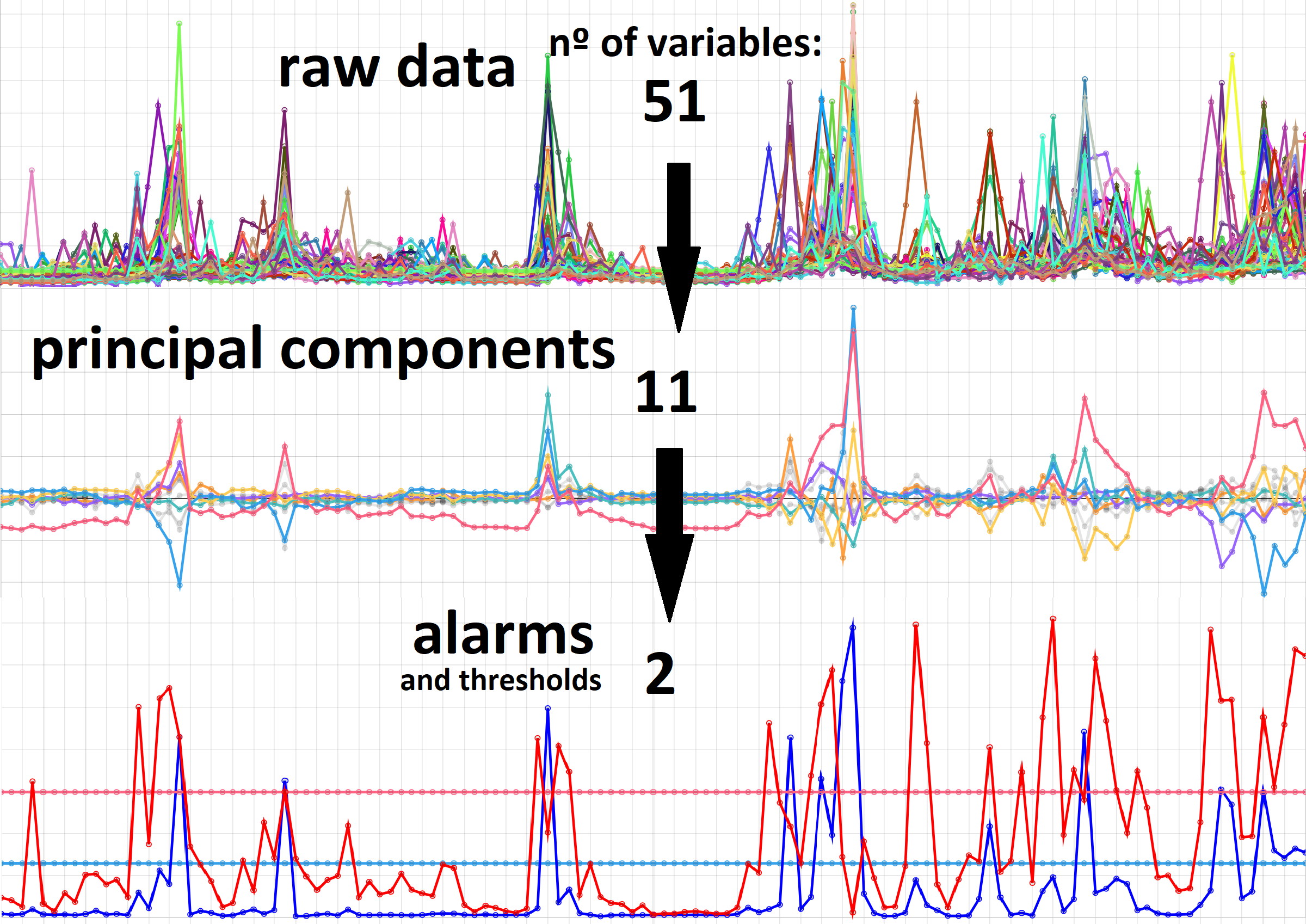
Abstract
We have created an alarm system for the Catalan Surveillance Network of SARS-CoV-2 in Sewage (SARSAIGUA). It is based on Principal Component Analysis (PCA). Two types of alarms are triggered: (1) when the measured concentration of SARS-CoV-2 is out of normality among all wastewater treatment plants, and (2) when one single plant decorrelates from the general trend (useful for early warning). The alarms are based on threshold trespassing of two well-known methods: Hotelling's T2 and Square Prediction Error (SPE or Q). A web-based interface has been implemented to facilitate the usage and visualization of the results.

Keywords: Principal Component Analysis (PCA), Fault Detection, Alarm System, SARS-CoV-2, Catalonia, Wastewater Based Surveillance.

Highlights
  1. A widely used technique in industry and chemometrics, applied to public health data.
  2. PCA allows separating the trends of the process and the noise into different subspaces.
  3. Alarm system based on threshold trespassing, calculated choosing significance level.
  4. Contribution analysis shows the influence of WWTPs responsible for abnormalities.
  5. A web-based interface implements the described procedure, so it can be executed in any browser as soon as the labs submit weekly PCR results into the SARSAIGUA platform.

Graphical Abstract

proposta: fer explícita la reducció de variables: de 51 a 11, i després de 11 a 2 (Q i T2)

Summary

1. Introduction

Surveillance networks of SARS-CoV-2 in sewage have been launched in many world countries. Each network selects multiple wastewater treatment plants, taking into account population, spatial coverage, and other technical and/or economic constraints. Once a network is launched, the data generated needs to be transformed into useful information to support decision making.

Analysing each WWTP separately makes it difficult to reach conclusions, hence statistical methods are needed to analyse at once all WWTP data generated from the network.

Catalonia is a region with more than 7.7 million inhabitants in north-eastern Spain. The Catalan Water Agency (ACA) and the Public Health Agency of Catalonia (ASPCAT) promoted and funded the deployment of the Catalan Surveillance Network of SARS-CoV-2 (SARSAIGUA, https://sarsaigua.icra.cat/) (Guerrero et al., 2022). This network started in July 2020 monitoring 56 WWTPs evenly distributed across Catalonia, serving 80% of the total population (7.5 million inhabitants). The sample collection and analysis started on July 6, 2020, approximately four months after the detection of the first clinic COVID-19 case in Catalonia (February 25, 2020). Out of the 532 WWTPs in Catalonia, 56 were included in the surveillance network; these 56 represent a high population coverage (80%) and are evenly distributed across the territory (at least 1 WWTP per county). The sample frequency was set to one sample per week in 36 of the selected 56 WWTPs and biweekly for the remaining 18, thus resulting in the collection and analysis of 45 samples per week. Remarkably, some WWTPs are only surveyed during the summer season to better monitor municipalities receiving high tourism (e.g., Castell-Platja d’Aro, Vilaseca-Salou). Refrigerated flow-based composite samples are collected for most WWTPs at the entrance. The 45 weekly samples are distributed to the three reference laboratories with wide expertise in molecular diagnosis and environmental virology. Each laboratory receives 15 samples per week that are analyzed for SARS-CoV-2 genome abundance using optimized protocols. Quantification of SARS-CoV-2 genomes is accomplished using RT-qPCR targeting a common genetic marker (N1) and two complementary targets, N2 and IP4. After 20 months of monitoring (from July 2020 to March 2022), SARSAIGUA has analyzed approximately 3,600 samples.

Herein we've applied Principal Component Analysis (PCA, a statistical process control technique) to the time series generated by all WWTPs which are part of SARSAIGUA. This facilitates the identification of single WWTP deviations from the normal behaviour (early warning) and global WWTP deviations from the normal behaviour (generalized outbreak).

2. Methods

2.1. Data sources

2.1.1 WWTP data

Input data used for this study is retrieved from our own API (created ad-hoc). It is available at https://apicovid.icradev.cat/n1. When accessed, the API reads our SQL database (where the labs submit the PCR results every week) and outputs the data in CSV format. The data includes information about the concentration of N1 gene copies at each WWTP and influent flows (in m3/day).

SARSAIGUA covers different plant sizes: from 1,698 to 1,484,787 inhabitants, and from 363 to 334,712 m3/day of average influent flows. In addition, the plants cover zones with different degrees of industrialization as well as with a different touristic pressure.

Manual data quality control on the lab results is executed weekly. This manual quality control involves evaluating: i) RT-qPCR standard curve parameters; ii) recovery values from process control and iii) correlation between RT-qPCR target genes. Whenever large deviations from previous accumulated data in parameters like recovery percentage of a process control are identified, the labs are requested to repeat the sample.

For the analysis, 51 WWTPs (see wwtps) were included which correspond to the ones sampled weekly and biweekly; the seasonal WWTPs (only sampled during winter or summer periods) were excluded from the analysis. The data used as input for the procedure applied in this study (PCA and 2 statistical tests) is the (N1 gene copies)/day/person; for each observation at each WWTP the concentration of N1 (GC/L) is multiplied by flow (L/day) and divided by the number of inhabitants serviced by that WWTP.

WWTP code Population (inhabitants) Average inflow (m3/day) Sampling frequency
DBSS 1,484,787 334,712 weekly
DPDL 1,154,006 204,328 weekly
DMIR 241,142 49,968 weekly
DTRS 227,825 39,389 weekly
DGVC 220,302 40,082 weekly
DSFL 206,708 48,307 weekly
DMAT 185,114 23,465 weekly
DGIR 146,609 41,619 weekly
DLLE 145,211 51,106 weekly
DSRS 135,228 22,943 weekly
DLLL 133,252 34,485 biweekly
DTAR 132,381 25,266 weekly
DRUS 108,581 15,655 weekly
DRUB 97,940 21,904 weekly
DGRA 97,393 21,138 weekly
DMAS 92,243 20,646 weekly
DVLG 80,910 15,554 weekly
DMDV 76,690 30,441 biweekly
DIGU 65,757 17,459 weekly
DABR 65,160 16,187 weekly
DVDP 62,122 14,006 weekly
DVIC 55,679 22,118 weekly
DPAM 55,339 14,984 weekly
DFIG 52,048 13,319 weekly
DVEN 49,850 11,398 weekly
DVLC 49,663 35,768 weekly (summer)
DOLO 40,127 15,273 weekly
DBLN 39,028 8,673 biweekly
DLDM 38,373 9,768 biweekly
DCPA 38,008 13,921 biweekly (summer)
DTOT 36,005 5,722 weekly
DMRT 35,801 7,731 weekly
DBAY 27,959 10,695 weekly
DMAN 27,898 5,307 weekly
DVAL 22,410 9,304 biweekly
DFON 22,005 22,208 biweekly
DAMP 20,738 3,964 weekly
DRSS 19,550 9,191 biweekly (summer)
DBAL 17,162 7,217 weekly
DTRG 17,098 3,284 biweekly
DBER 16,494 4,616 weekly
DMOF 15,185 3,376 weekly
DPUI 15,120 6,790 weekly
DRIP 13,695 7,696 weekly
DSLL 12,356 2,490 weekly
DSOL 9,509 2,367 weekly
DCER 9,180 1,469 biweekly
DMLN 8,777 1,616 biweekly
DMOB 7,364 1,109 biweekly
DBBL 6,087 1,774 biweekly
DTRP 5,845 2,145 biweekly
DVIE 4,892 6,799 biweekly
DGAN 3,064 525 biweekly
DFAL 2,834 363 weekly (winter)
DPSU 2,220 1,026 biweekly
DSOR 1,698 462 biweekly
total 5,958,422 1,363,128
wwtps WWTPs of the SARSAIGUA surveillance network sorted by amount of serviced population. Also, average influent flows are displayed.

2.1.2 Clinical cases

A second input dataset has been prepared: daily reported clinical cases for all municipalites served by each WWTP, weighted by the percentage of inhabitants connected to each WWTP. This data was extracted from the official API of the Information Systems of the Department of Health and the Catalan Health Service (https://analisi.transparenciacatalunya.cat/resource/jj6z-iyrp.json).

The percentage of each municipality's inhabitants connected to each WWTP was requested directly to WWTPs. This information is available here: https://covidvigilancia.icra.cat/formularis/municipis_assistits.json

2.2. Gap filling

An input matrix without gaps is required when running PCA. Linear interpolation has been applied to the biweekly-sampled WWTPs (N1 concentration and flows) and missing values due to incidences in sampling (e.g., missing flow data).

2.3. Principal Component Analysis

Principal Component Analysis (PCA) is a multivariant statistical method for exploratory data analysis (unsupervised learning). It can be used to reduce the number of variables in a dataset while retaining as much information as possible.

PCA works by transforming the original variables into a new set of variables, called principal components, which are uncorrelated and ranked in order of importance. These new variables are linear combinations of the original variables: the first principal component is the linear combination that captures the greatest amount of variation in the data. The second principal component is the linear combination that captures the next greatest amount of variation in the data, subject to the constraint that it is orthogonal (i.e., perpendicular) to the first principal component, and so on for the remaining principal components.

PCA can be used for a variety of applications, such as identifying patterns, reducing the dimensionality of data for visualization, and making predictions using machine learning algorithms.

Our goal in this study is to use PCA as a basis for an automated alarm sytem procedure, based on fault detection techniques: (1) the error of reprojection (Squared Prediction Error, SPE or Q), which we've identified as useful for early warning, and (2), the Hotelling's T2, which has the ability to detect shifts in the mean vector of a process; in our case identifies abrupt increases in the general circulation of the virus.

2.3.1. Pretreatment

Let X be a complete matrix, containing n observations (rows) and m variables (columns).

obs nº WWTP[1] WWTP[2] ... WWTP[m]
X= 1 ... ... ... ...
2 ... ... ... ...
... ... ... ... ...
n ... ... ... ...

Scaling is performed to each column, to ensure each WWTP is given equal weight in the monitoring process. Involves subtracting each variable by its sample mean (to capture the variation from this mean) and then, divide by its standard deviation. This gives equal importance to all columns (no matter the size) and also removes variabilities caused by different sampling and analytical methods (e.g. analytical differences between labs).

2.3.2. Covariance and correlation matrix

Let S be the covariance matrix of X. Since X is mean centered, it can be calculated as:

\[ S = \frac{1}{n-1} X^T X \]

S is also the correlation matrix because X is scaled to unit variance. Size of S is mxm.

2.3.3. Eigenvalues and eigenvectors

A Single Value Decomposition (SVD) algorithm is applied to S: \[ S = V \Lambda V^T \]

  • V is an orthogonal matrix (VTV=I). Its columns are called the "loading" vectors (or eigenvectors). Size is mxm.
  • Λ is a diagonal matrix (size mxm) that contains the non-negative real eigenvalues of decreasing magnitude along its main diagonal, and zeros in the offdiagonal elements: \[ \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_m \ge 0 \]

2.3.4. Loadings and scores

Let x be any row of X (an observation vector, size m). Let t be the projection of x into the matrix V: \[ t = xV \]

Projecting into x into V decouples the observation space into a new set of uncorrelated variables (the elements of t):

The ith column of V is the loading vector pi that transforms an observation x into the "score" t.

To distinguish between the transformed variables and the transformed observations, the transformed variables are called "principal components" and the individual transformed observations are the "scores".

2.3.5. Reducing dimensionality

Let a be an integer value between 1 and m. Let P be the matrix resulting from taking the first a columns of V, corresponding to the a largest eigenvalues of S. P size is mxa. \[ P = [V_1,...,V_a] \]

Choosing the value of a is choosing the number of principal components. This choice can be done in multiple ways. In this study we've chosen the number of principal components corresponding to the eigenvalues of S larger than one, which is the same as keeping only the principal components with variance above the average.

Let T be the projection of X into P, also known as the "scores" matrix. T size is nxa. \[ T = XP \]

2.3.6. Properties

Let Ti be the ith column of T. The following properties can be shown:

  • Ordered variance: Var(T1) ≥ Var(T2) ≥ ... ≥ Var(Ta) .
  • Mean of Ti is 0 for all i.
  • All components are orthogonal (Ti·Tj=0 for all i≠j).
  • There exists no other orthogonal expansion that captures more variation of the data (using a components).

2.3.7. Residual matrix

Let X̂ be the matrix resulting of projecting T back into the original m-dimensional space. Size of X̂ is nxm: \[ \hat{X} = TP^T \]

Let E be the residual matrix, computed from the difference between the original X and the back-projection of T. Size of E is nxm: \[ E = X - \hat{X} \]

2.4. Fault detection

Dimensional reduction provided by PCA (from m to a variables) represents nearly the same information in a lower dimension space. This new space can be used for multivariate process monitoring.

The Hotelling's T2 statistic uses the a-dimension space (columns of the matrix T) to detect misbehaviours based on threshold trespassing.

The Q statistic uses the residual matrix (E) to monitor the portion of observation corresponding to the smallest eigenvalues of S (from number a to m).

2.4.1. Hotelling's T2

For every observation in the reduced space (t) we can associate a T2 value, computed as:

\[ T^2 = \sum_{i=1}^{a}{ t_i \lambda_i^{-1} t_i^T } \]

The value of T2 can be interpreted as the distance of this observation to the center of the model (mean).

Scores are scaled inversely proportional to the standard deviation along the eigenvectors (columns of P). This allows defining a scalar threshold to characterise the variability in the a-dimensional space.

Given a level of significance (α, chosen as 0.05 in this study), appropriate threshold values for the T2 statistic can be determined. When the mean and variance are estimated from a sample of observations, the threshold is calculated as:

\[ T_\alpha^2 = \frac{a(n+1)(n-1)}{n(n-a)} F_\alpha(a,n-a) \] Where:
  • \[ F_\alpha(v_1,v_2) = \frac{\chi^2(v_1)/v_1}{\chi^2(v_2)/v_2} \]
  • v1=a and v2=n-a: are the degrees of freedom.
  • Fα(v1,v2) is the inverse F distribution function (Fisher-Snedecor).
  • α is also the ratio of false alarms.

2.4.2. Prediction error (Q or SPE)

Let r be the residual vector of an observation (x), computed from the back projection of its scores in the lower dimensional space. \[ r = x-\hat{x} \] \[ r = x-tP^T \] \[ r = x-xPP^T \] \[ r = x(I-PP^T) \] The Squared Prediction error (SPE) or Q statistic of an observation can be computed as: \[ Q = rr^T \] A threshold (Qα) can be defined as: \[ Q_\alpha = \theta_1 ( \frac{ c_{1-\alpha} h_0 \sqrt{2\theta_2} }{\theta_1} + 1 + \frac{ \theta_2 h_0 (h_0-1) }{ \theta_1^2 } )^{\frac{1}{h_0}} \] Where:

  • c1-α = boundary value that determines the area 1-α with mean=0 and standard deviation=1 in the normal distribution.
    For example: c0.95 = 1.644854 (in R can be computed as qnorm(0.95,0,1)).
  • \[ \theta_i = \sum_{j=a+1}^{m}{ \lambda_j^i } \]
  • \[ h_0 = 1 -2\theta_1 \frac{\theta_3}{3\theta_2^2} \]

2.4.3. Contribution analysis

The T2 chart is useful to detect observations out of normal operation conditions. It is a quality measure of the data according to the model (the first a principal components). It is measured in the direction of the model. If T2 increases, the observation preserves the model structure but with larger values ("far from the mean").

The Q chart detects structural changes in the process. It is a measure of the projection error. It is measured in the error direction (orthogonal to PCs). If Q increases, the correlation structure gathered by the PCA model (the first a components) is not preserved in that observation.

Contribution analysis answers which variable/s in the original space are responsible of the detected fault (threshold trespassing), which we refer to as "alarms" in our study.

2.4.3.1. Contribution analysis for T2

For one observation under fault, the contribution of one particular variable from the original space to the out of control status is: \[ T^2_{contribution_j} = \sum_{k=0}^{a} \frac{t_k}{\lambda_k}p_{kj} x_j \] Where:

  • j = number of the variable from the original (m-dimensional) space.
  • k = number of the variable from the transformed (a-dimensional) space.
  • λj = kth largest eigenvalue of S.
  • xj = jth element of the obseravation vector x.
  • tk = kth element of the scores vector t.
  • pkj = kth, jth element of P.

2.4.3.2. Contribution analysis for Q

For one observation vector x under fault, the components of the residual vector r are directly the contributions to Q. \[ Q_{contribution_j} = r_j \]

2.5. Implementation in a web interface

All the equations above have been implemented in Javascript. This language choice allows doing all the computation client-side, since it is native in all web browsers (e.g. Google Chrome, Mozilla Firefox, Microsoft Edge, etc.), regardless of the operating system, and type of device.

The starting point was creating a matrix library from scratch, to perform basic matrix operations (e.g., sum, multiplication, transposition, determinant, inverse...). Then, the SVD algorithm and PCA procedures were implemented. Then the Hotelling T2 and Q statistics, along with the calculation of the contributions.

This matrix library is freely available at https://github.com/icra/matrix-library-js, but at the time of this writing is still not fully documented.

To validate the Javascript implementation, numeric tests were conducted using R (https://www.r-project.org/) since it is a well-known and stablished numeric platform with PCA functions builtin.

The matrix library was then loaded into the web interface, also created ad-hoc, coded in HTML and CSS, and using VueJS (https://vuejs.org/) as the frontend Javascript framework. This approach was selected to facilitate the integration of these developments with the SARSAIGUA platform as a superior layer of analysis, beyond current visualization options.

3. Results and Discussion

3.1. Raw time series (input data)

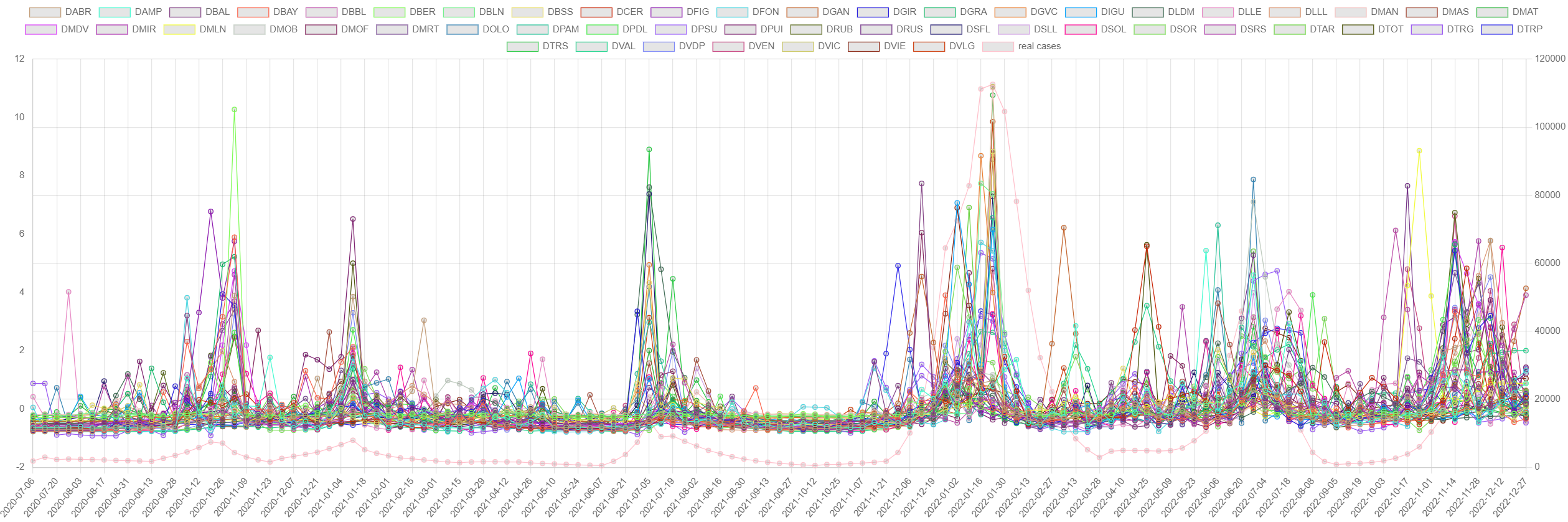
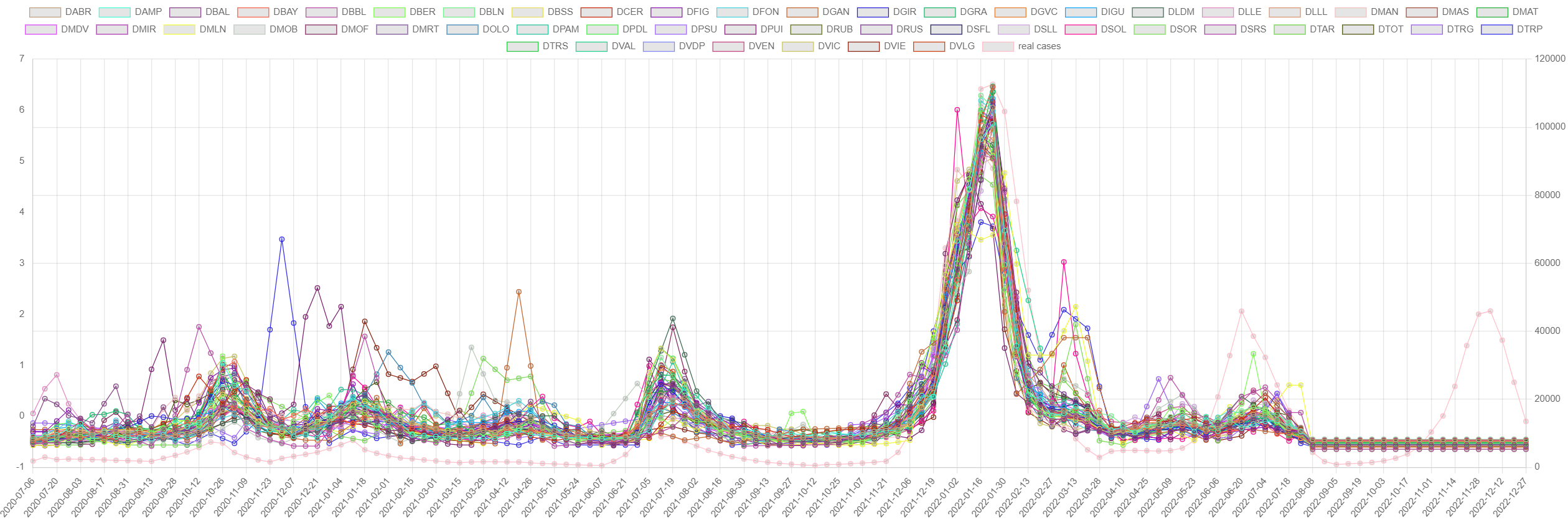
The evolution of the COVID-19 pandemic in Catalonia can be observed in raw and raw_cases. Between March 2020 and December 2022, seven waves have hit the Catalan population. The first wave started in March 2020, but it is out of the scope of the SARSAIGUA program. The evolution in terms of waves is both explained by reported cases and N1 loads detected in wastewater; the Spearman correlation between both signals is of 0.69, using data until the 6th wave. In the April 2022 the government stopped progressively reporting positive COVID-19 cases and launched a sentinel system based on screening of certain patients in key primary care health centres.

The most dominant variant of SARS-CoV-2 have been: Delta (until January 2022), Omicron BA.1 (until mid-March 2022), Omicron BA.2 (until mid-June 2022), Omicron BA.4 and BA.5 (until November 2022), and Omicron BQ.1 (current at the time of this writing).

raw Time series: N1 (CG/inhabitant) at each WWTP, from July 2020 to December 2022. Each WWTP is mean centered and scaled to unit variance.

raw_cases Time series: reported clinical cases per 1000 inhabitants at the municipalities served by each WWTP, from July 2020 to April 2022. Each WWTP is mean centered and scaled to unit variance.

3.2. PCA results

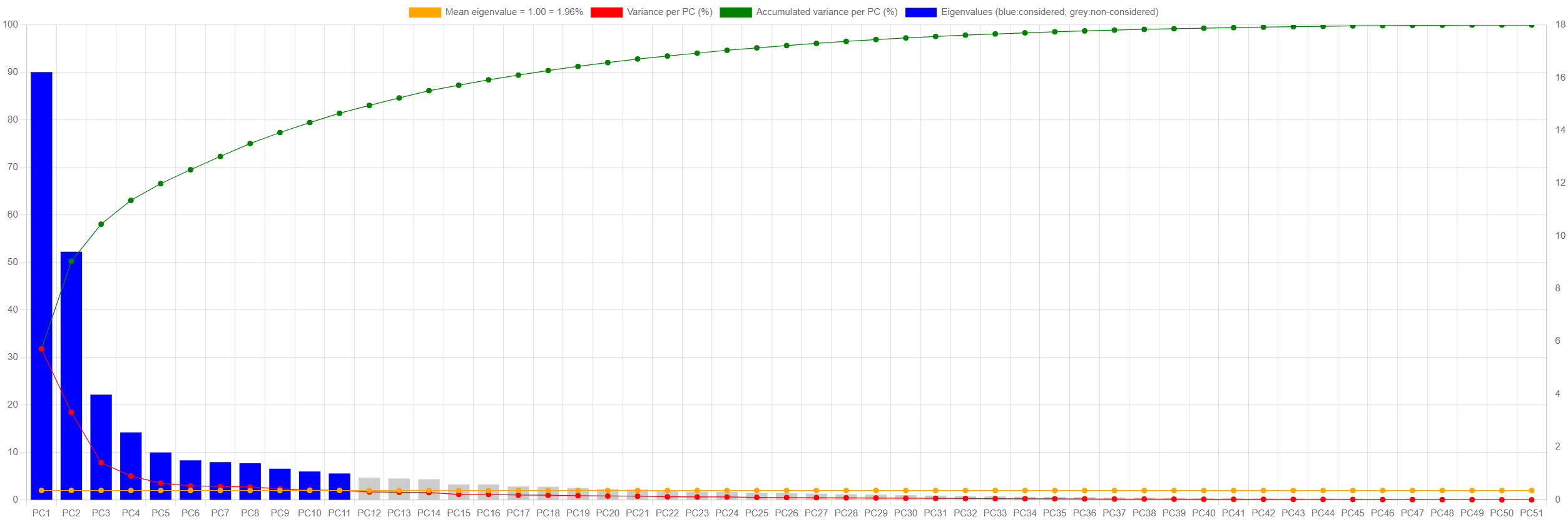
PCA of N1/inhabitant was run with an input matrix X of 125 observations (rows) and 51 WWTPs (columns). Taking 11 PCs (with associated eigenvalue>1), 82% of the variance was retained (see eigenvalues).

loadings_and_scores (left) shows the loadings from PC1 vs PC2. All WWTPs contribute positively to PC1; no clear clustering exists. But PC2 shows some clusters: (1) WWTPs with positive contribution to PC2 and (2) WWTPs with negative contribution to PC2.

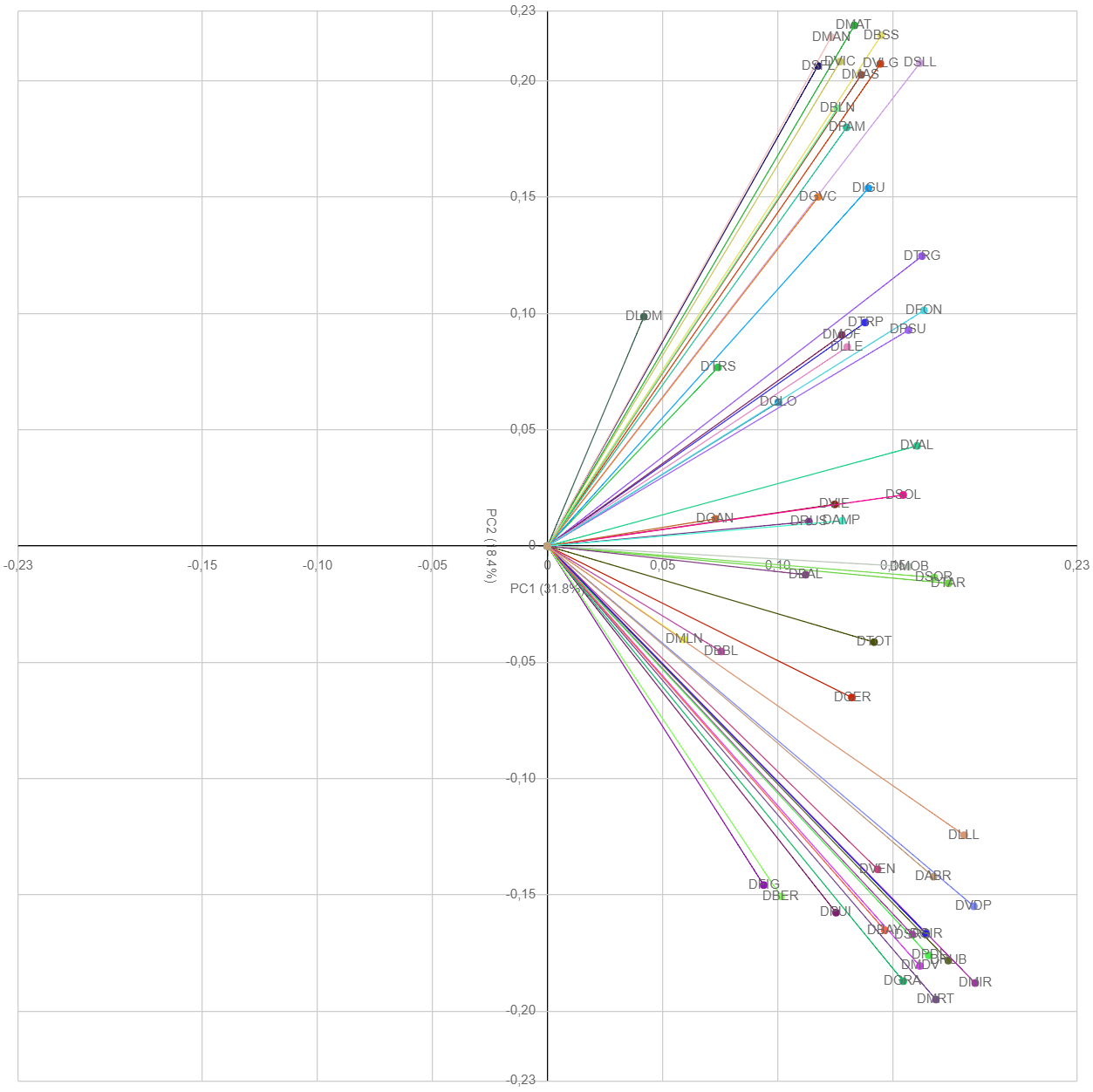
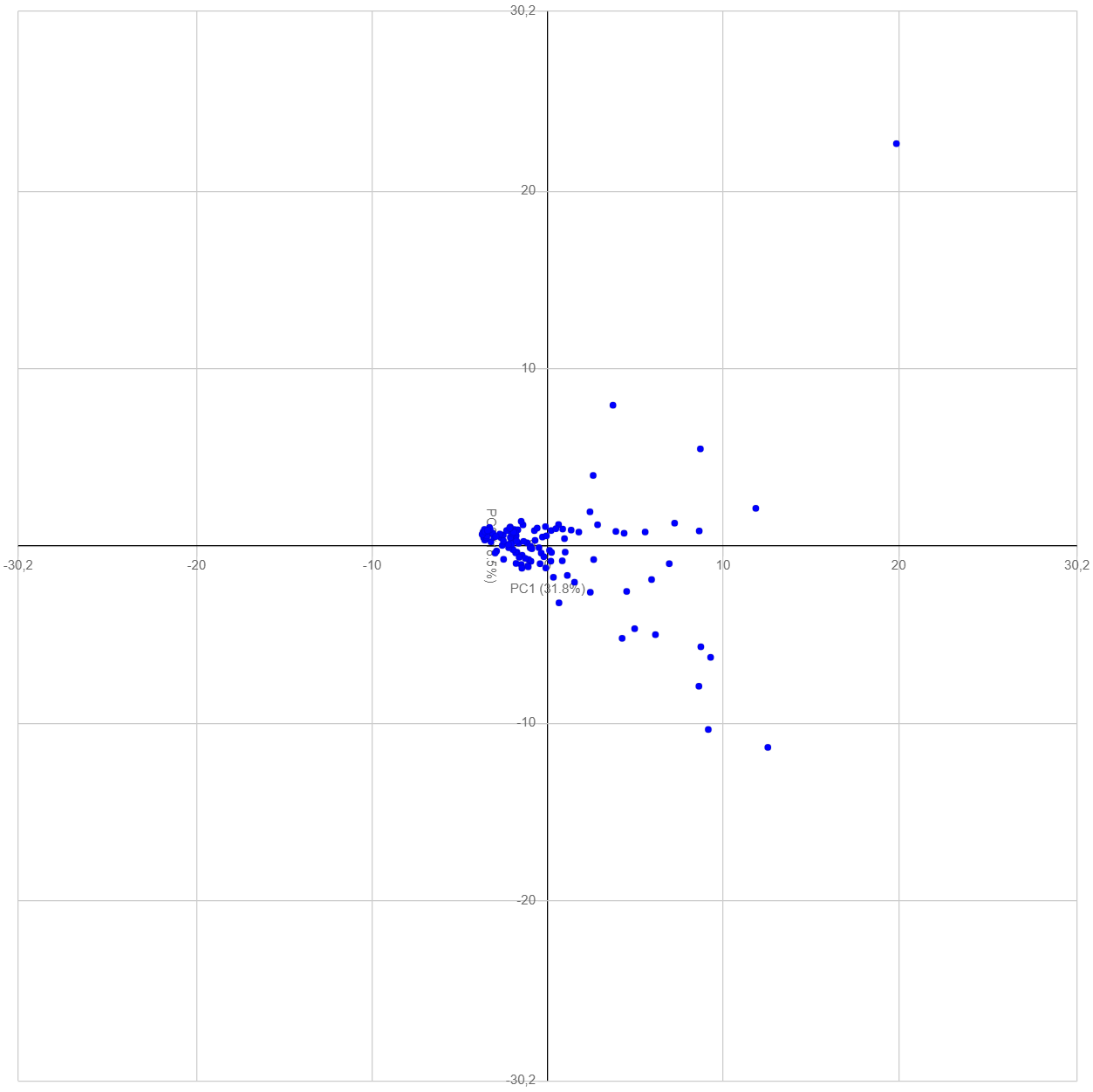
PC1 explains 32% of the variance. This signal is equivalent to the mean of each observation (after scaling it with the standard deviation of the first principal component).

PC2 explains 18% of the variance and distributes WWTPs along the vertical axis. PC2 captures differences amongst WWTP groups. In particular, PC2 clusters WWTPs that did not detect 2nd, 3rd and 7th wave very well, but had a very strong detection of 4th, 5th and 6th wave, and the other cluster is the opposite (see clusters_PC2).

eigenvalues Eigenvalues, percent variance explained per PC and accumulated variance per PC.

loadings_and_scores Loadings and Scores (PC1 vs PC2).

scores Scores (time series) of the first 11 principal components.

clusters_PC2 Time series of PC2's scores (purple), with raw data of WWTPs with positive contribution to PC2 (red), and raw data of WWTPs with negative contribution to PC2 (blue). Blue lines have been "mirrored" respect the horizontal (x) axis (multiplied by -1), so they can be seen without overlaping with the red lines.

3.3. Detection of outbreaks

3.3.1. Control charts

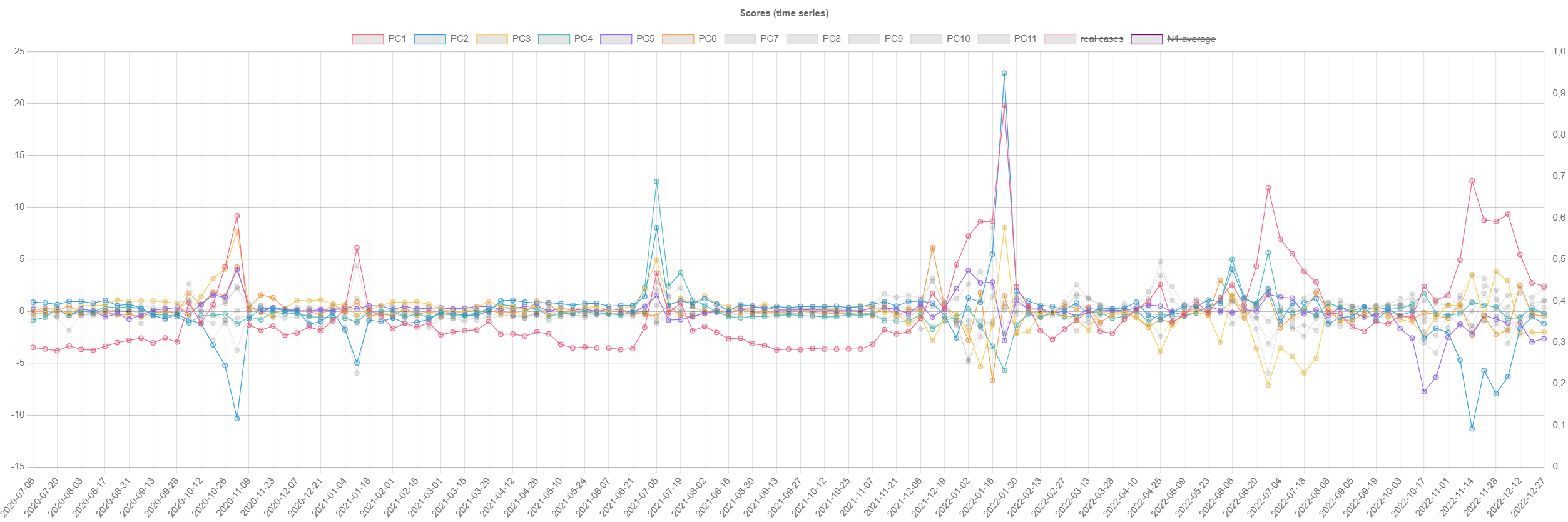
TO DO

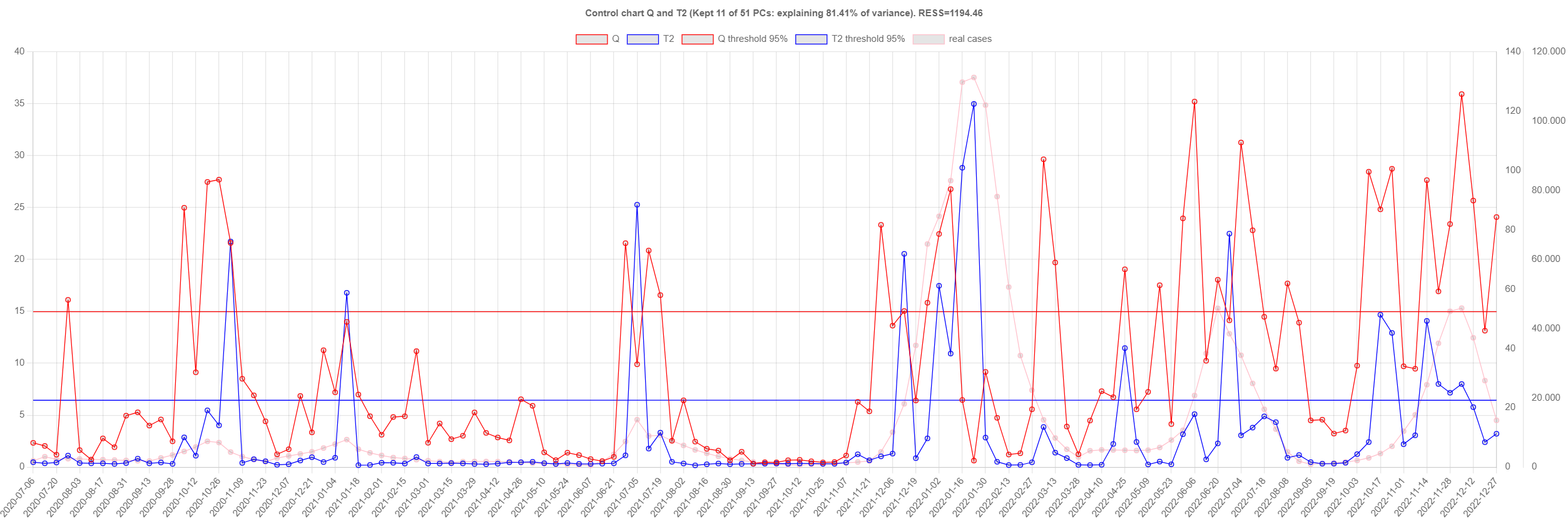
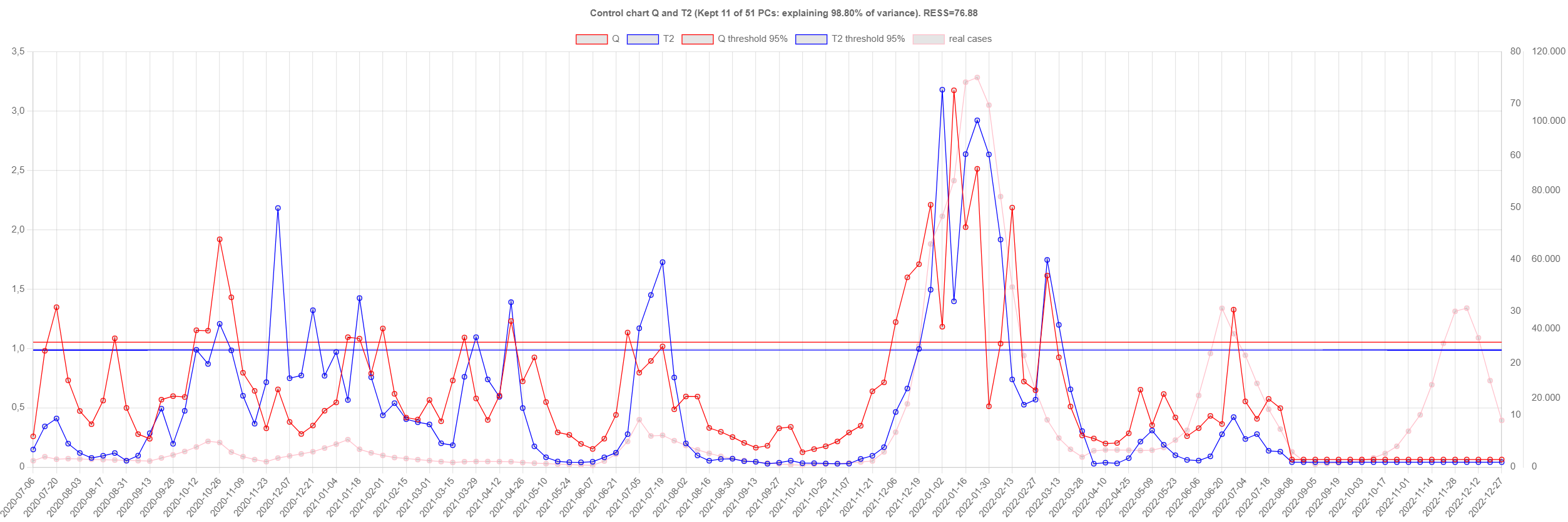
control_charts Control chart (top: N1/inhabitant, bottom: clinical cases) with Q and T2 and respective thresholds. Note that reporting of cases stopped on 2022-08-01.

3.3.2. Contributions of the different WWTPs to Q and T2 alarms

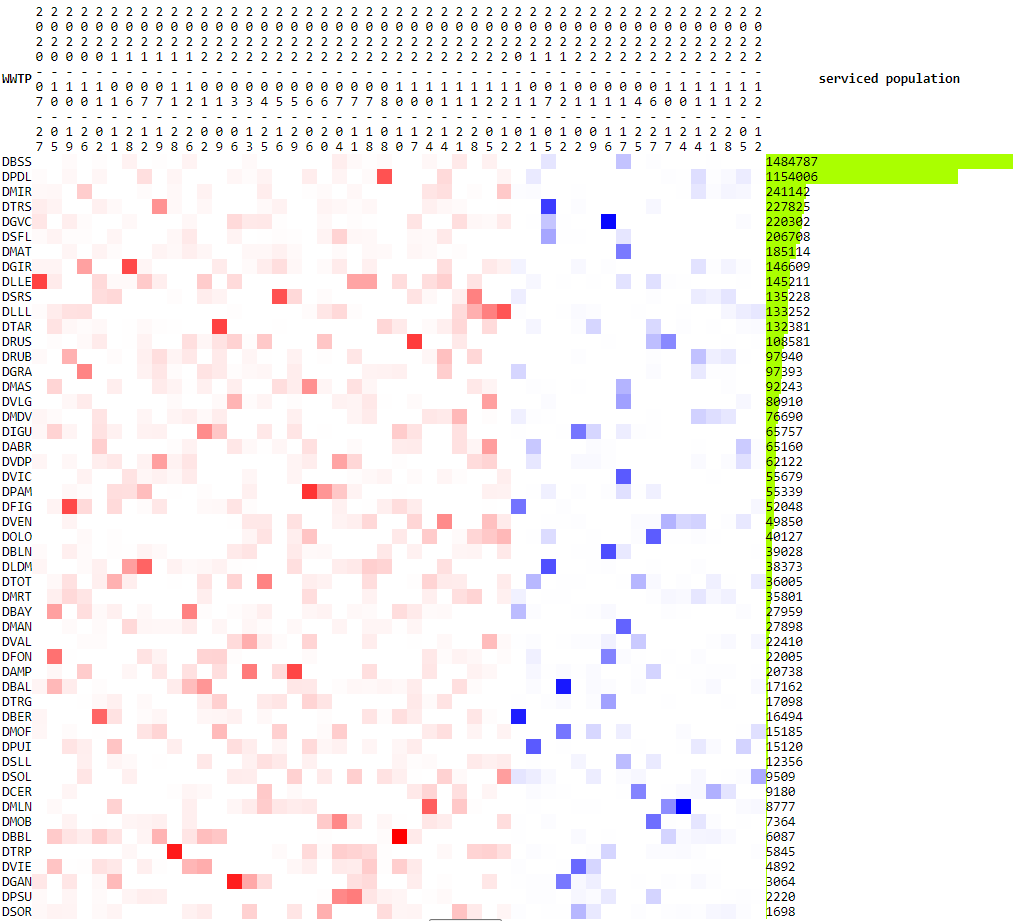
One might wonder if the same subset of WWTPs is consistently triggering alarms; the response is not. contributions shows the contribution of each WWTP to each alarm. The triggering of alarms is generated by different subsets of WWTPs. In the case of T2, the fact that some WWTPs contribute little to trigger alarms means that these follow the general pattern of N1 concentrations (WWTPs pushing towards the center of the 11-dimensional space); in general these are either the larger WWTPs (DPDL or DBSS) or the ones closer to the Barcelona region (mobility in Catalonia is dominated by trips from and to the Barcelona region). With regards to the Q-statistic, we cannot see a clear subgroup of WWTPs prone to earlier detect outbreaks (higher sensitivity in detecting changes in N1 concentrations).

contributions Contributions to alarms by each WWTP, sorted by serviced population in descending order. Intensity of color is with respect to the highest contribution among all alarms. Red cells correspond to alarms for Q. Blue cells correspond to alarms for T2.

The fact that the Q alarms when executed on the clinical reported cases and on wastewater match well, indicates that the ranking in the Q-statistic is more related to the spread of each wave across the territory rather than the sensitivity of the WWTPs. It is also possible that sampling or analytical errors lead to unexpectedly higher or smaller N1 concentrations; such poor data quality values would influence the result of the PCA and trigger false alarms. The developed system allows detecting such abnormal behaviour and tracing back the origin of the alarm to a single WWTP (in that case). Hence, a manual check is needed for each alarm generated, and if generated by a single WWTP or by WWTPs analyzed by a single laboratory, a verification of data quality needs to be conducted before triggering an alarm and communicating to health authorities.

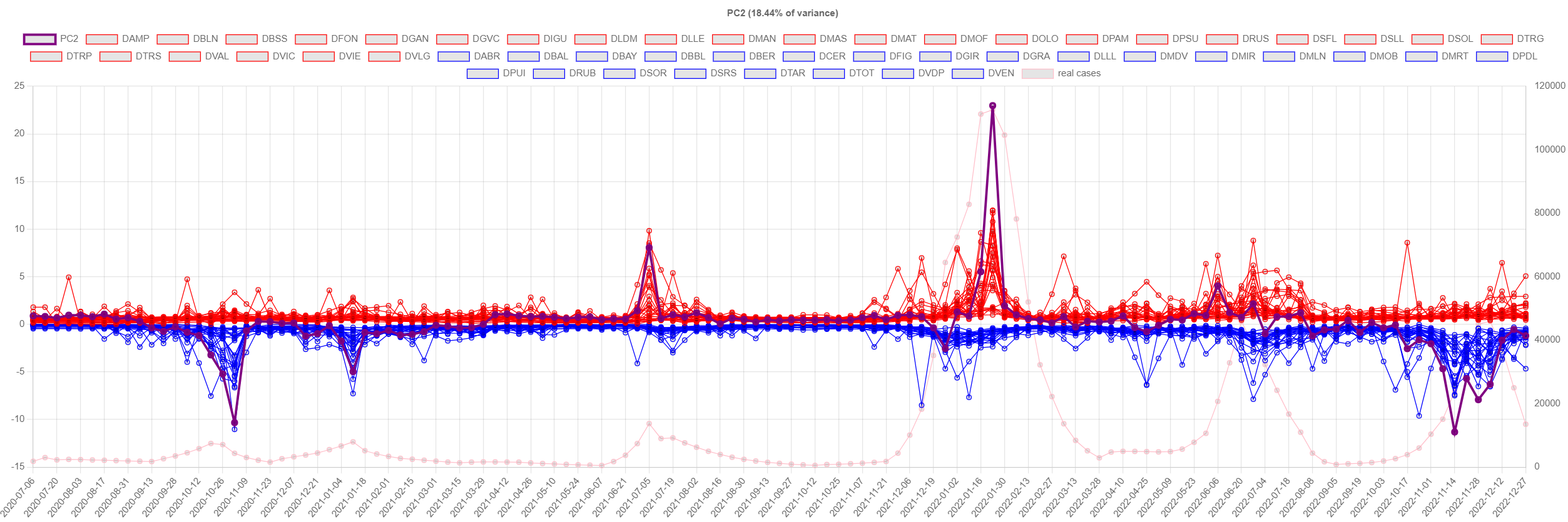
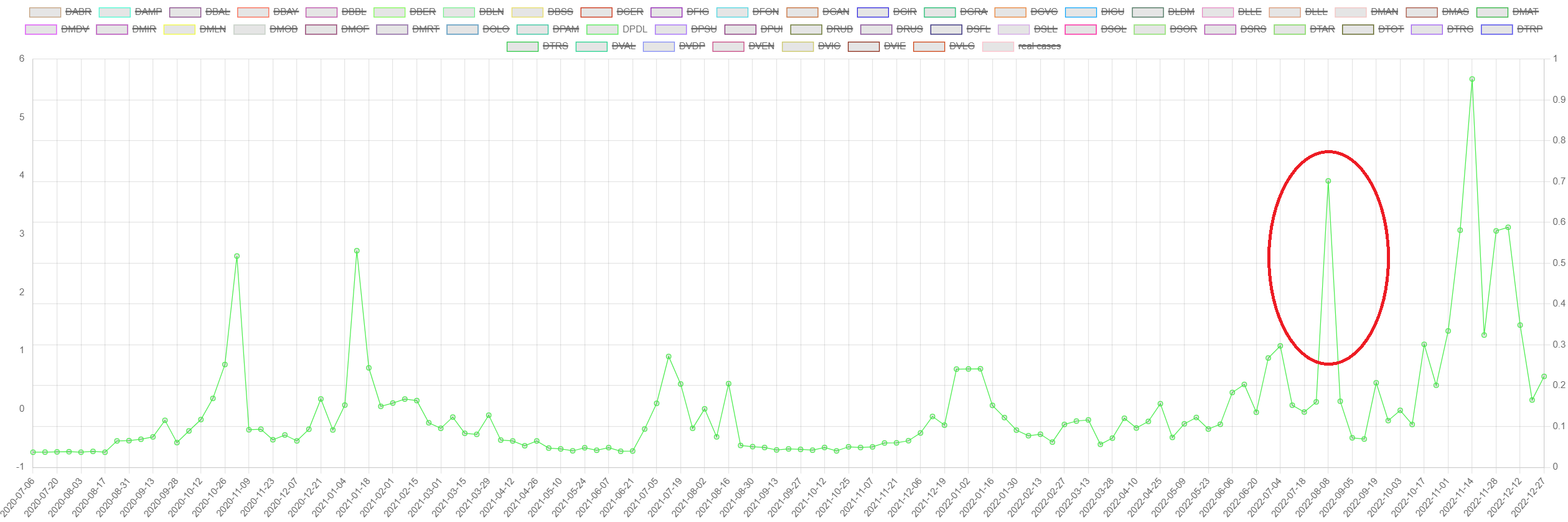
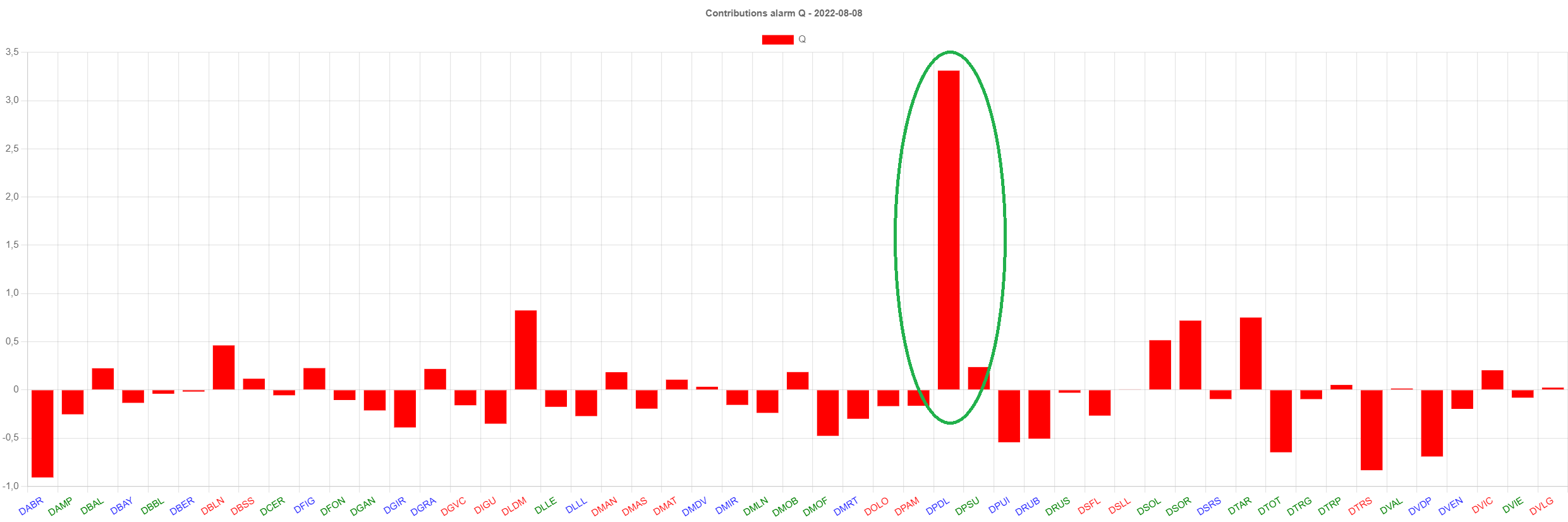
Such a situation happened in one observation, where an unexpected increase was observed (observation at 2022-08-08 for the WWTP "DPDL", see outlier). All analytical parameters were within the quality control ranges; the only explanation was the potential discharge of sewage from cruise ships which discharge to the WWTP of DPDL. Yet, the system allowed identifying such abnormal behaviour and go back to revise data quality from that observation. Overall, the message is that the more WWTPs included in a surveillance network the better. The method proposed in this paper allows capturing relevant information from all WWTPs included in a surveillance network to anticipate outbreaks.

outlier Values of N1/inhabitant at WWTP "DPDL". It spikes at 2022-08-08. The alarm system triggers an alarm for Q. Below, the contribution decomposition by WWTP for the alarm triggered at that day. It reveals that the largest contribution by far was almost entirely by that WWTP.

4. Conclusions

punts clau:

5. References
    rendering...

6. Acknowledgements and others

 TO DO

7. Appendix

 TO DO